题目描述
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
示例 1:
1
2
3
4
5
| 输入:n = 2
输出:2
解释:有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶
|
示例 2:
1
2
3
4
5
6
| 输入:n = 3
输出:3
解释:有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶
|
提示:
题解
该题就是找规律,只要找到规律,写出来不难,下图中列举了从1到5阶楼梯的走法。
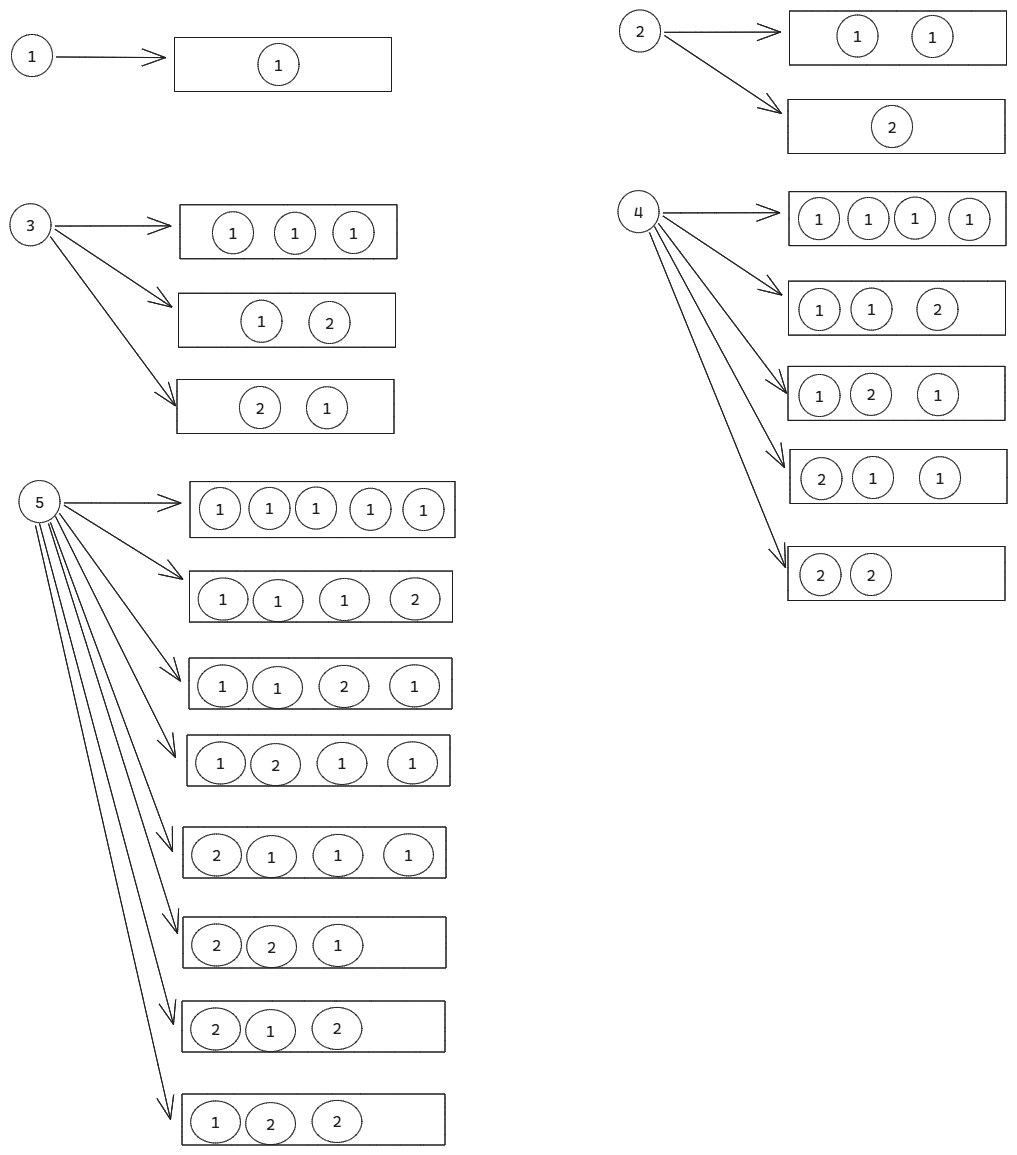
可以得到如下结论:
1
2
3
4
5
6
| 台阶数 走法
1 1
2 2
3 3
4 5
5 8
|
能得到如下结论:
N阶楼梯的走法 = N - 1阶楼梯的走法 + N - 2阶楼梯的走法
可以使用递归实现:
1
2
3
4
5
6
7
8
| class Solution {
public int climbStairs(int n) {
if (n == 1 || n == 2) {
return n;
}
return climbStairs(n - 1) + climbStairs(n - 2);
}
}
|
提交:

很遗憾,超时了!递归会有栈溢出的情况,此题要修改为动态规划来解决。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution {
public int climbStairs(int n) {
if (n == 1 || n == 2) {
return n;
}
int p1 = 0, p2 = 1;
int r = 0;
for (int i = 3; i <= n; i++) {
r = p1 + p2;
p1 = p2;
p2 = r;
}
return r;
}
}
|
再次提交:
其实还可以再优化下,可以将n=1和n=2的情况与N>=3的情况统一。
1
2
3
4
5
6
7
8
9
10
11
12
| class Solution {
public int climbStairs(int n) {
int p1 = 0, p2 = 0;
int r = 1;
for (int i = 1; i <= n; i++) {
p1 = p2;
p2 = r;
r = p1 + p2;
}
return r;
}
}
|


