1.两数之和

题目描述

给定一个整数数组 nums 和一个整数目标值 target，请你在该数组中找出 和为目标值 target 的那 两个 整数，并返回它们的数组下标。

你可以假设每种输入只会对应一个答案。但是，数组中同一个元素在答案里不能重复出现。

你可以按任意顺序返回答案。

示例 1：

输入：nums = [2,7,11,15], target = 9
输出：[0,1]
解释：因为 nums[0] + nums[1] == 9 ，返回 [0, 1] 。

示例 2：

输入：nums = [3,2,4], target = 6
输出：[1,2]

示例 3：

输入：nums = [3,3], target = 6
输出：[0,1]

提示：

• 2 <= nums.length <= 104

• -109 <= nums[i] <= 109

• -109 <= target <= 109

• 只会存在一个有效答案

**进阶：**你可以想出一个时间复杂度小于 O(n2) 的算法吗？

题解

「暴力解法」

两层循环，第一层循环定义指针i指向每一个元素，第二层循环定义指针j指向每一个元素，比较nums[i] + nums[j]和target，如果相等则退出循环，返回[i, j]。

class Solution {
    public int[] twoSum(int[] nums, int target) {
       for (int i = 0; i < nums.length - 1; i++) { //如果是最后一个元素，则无需再向后比较，所以此处i < nums.length - 1
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[i] + nums[j] == target) {
                    return new int[]{i, j};
                }
            }
        }
        return new int[0];
    }
}

时间复杂度是O(n²)，空间复杂度是O(1)。

提交看下：

时间复杂度太高。

「Hash表」

我们可以借助hash表，以一个具体的用例来解答解释。

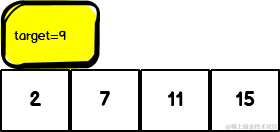
使用for循环：

1. 当i = 0的时候，计算target - nums[i] = 7在hash表中有没有，此时肯定是没有的，那么就将数据存储到hash表中，KV如何存储呢？K=(nums[i] = 2)，value=i。
2. 当i = 1的时候，同样计算target - nums[i] = 2，再次查看hash表中有没有2，此时hash表中有2，所以通过key=2，获取hash中对应的value，与当下的i做成一个数组，得到[0, 1]。

class Solution {
    public int[] twoSum(int[] nums, int target) {
        // map存储`[nums[i], i]
        Map<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < nums.length; i++) {
            int v = target - nums[i];
            // 去hash表中查询是否存在v
            if (map.containsKey(v)) {
                return new int[]{map.get(v), i};
            }
            map.put(nums[i], i);
        }
        return new int[0];
    }
}

提交：

可以看到时间上确实是快了，但是空间占用多了点，这是典型的空间换时间的方法，空间复杂度是O(n)，时间复杂度也是O(n)。